• Back to Profile
    •  

     


    When one particular species of event has always … been conjoined with another,
    we make no longer any scruple of foretelling one upon the appearance of the other,
    and of employing that reasoning, which can alone assure us of any matter of fact or existence.
    We then call the one object, Cause; the other, Effect.
    - David Hume's (1748, §7) An Enquiry Concerning Human Understanding

     

     

     

     

    Rubin Causal Model

    Treatments & outcomes


    Donald Rubin


    Jerzy Neyman

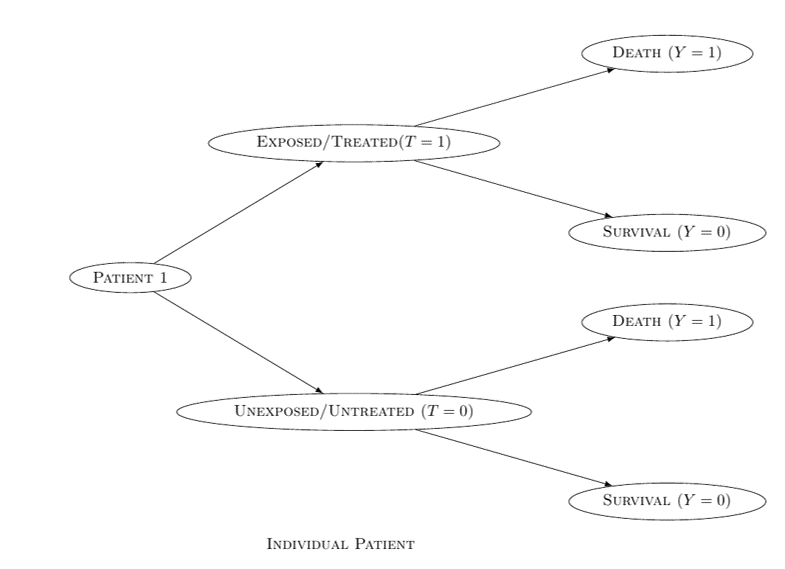
    The Rubin Causal Model is also known as the Neyman-Rubin Causal Model or Potential Outcomes Approach

    According to the Rubin Causal Model (Neyman, 1923, Rubin, 1974, Holland & Rubin, 1983, Robins, 1986, Hernán & Robins, 2020):
    A treatment T has a causal effect on the healthcare outcome Y, if there is a difference between the two potential outcomes YT = 0 and YT = 1
    Otherwise, T has no causal effect on Y

    1. In a clinical scenario:
    2. An individual patient will either be treated (T = 1) or remain untreated (T = 0)
    3. Whether T = 1 or T = 0, there are two outcomes: survival (Y = 0) or death (Y = 1)


    The fundamental problem of causal inference:
    1. Only one of the outcomes is observed for each individual: either the outcome if treated (YT = 1) or the outcome if untreated (YT = 0)
    2. ∴ Individual causal effects cannot be expressed as a function of the observed data because of missing data
    3. ∴ Identifying individual causal effects is generally impossible
    4. Nonetheless, we aim to identify the average causal effect in a population of interest



    EXAMPLE 1: Zeus (Hernán, 2004)

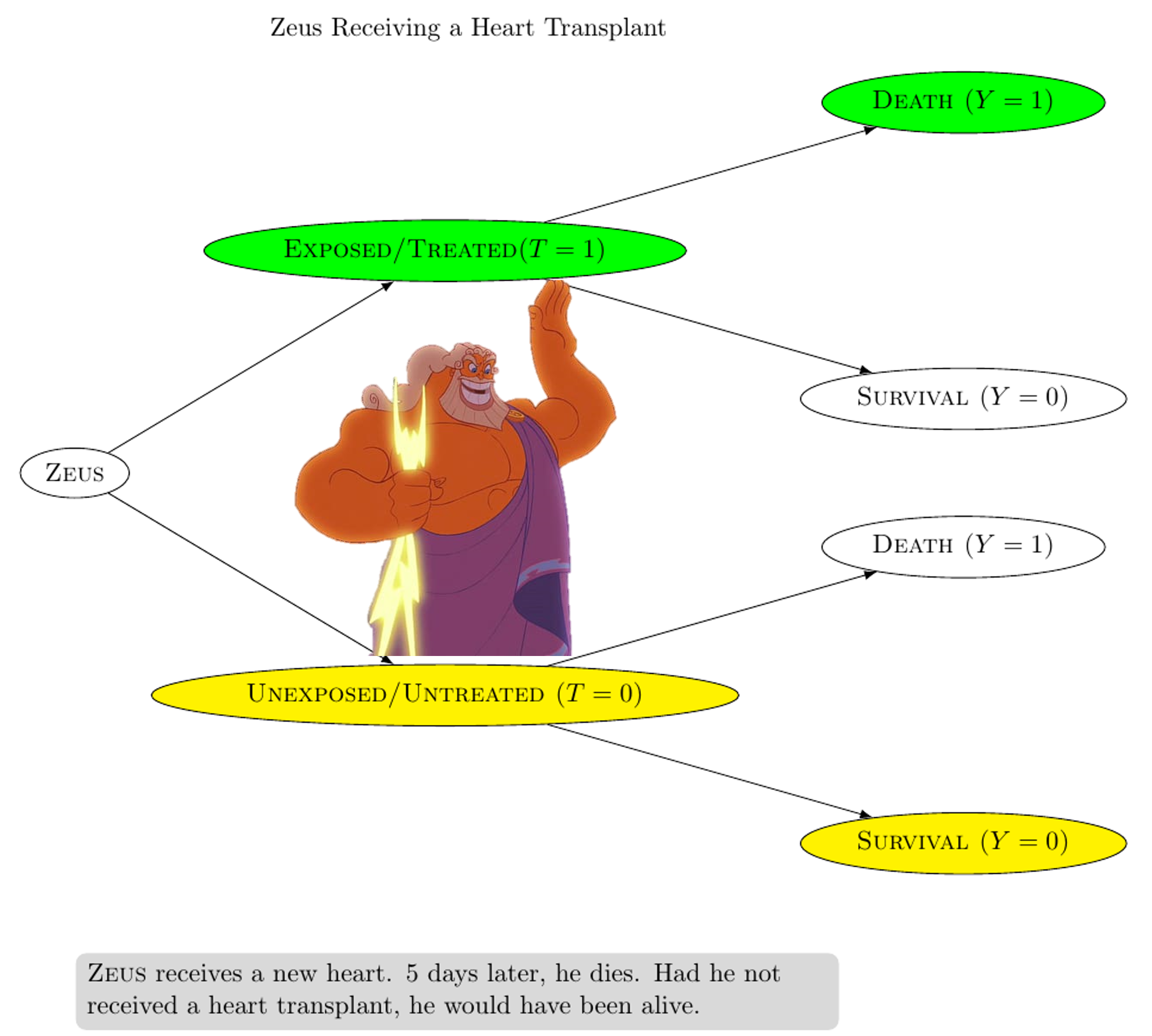
    In EXAMPLE 1, Zeus receives a heart transplant (T = 1)
    5 days later, Zeus dies (Y = 1)
    Had Zeus not received a heart transplant, he would have been alive (i.e. YT = 0 = 0)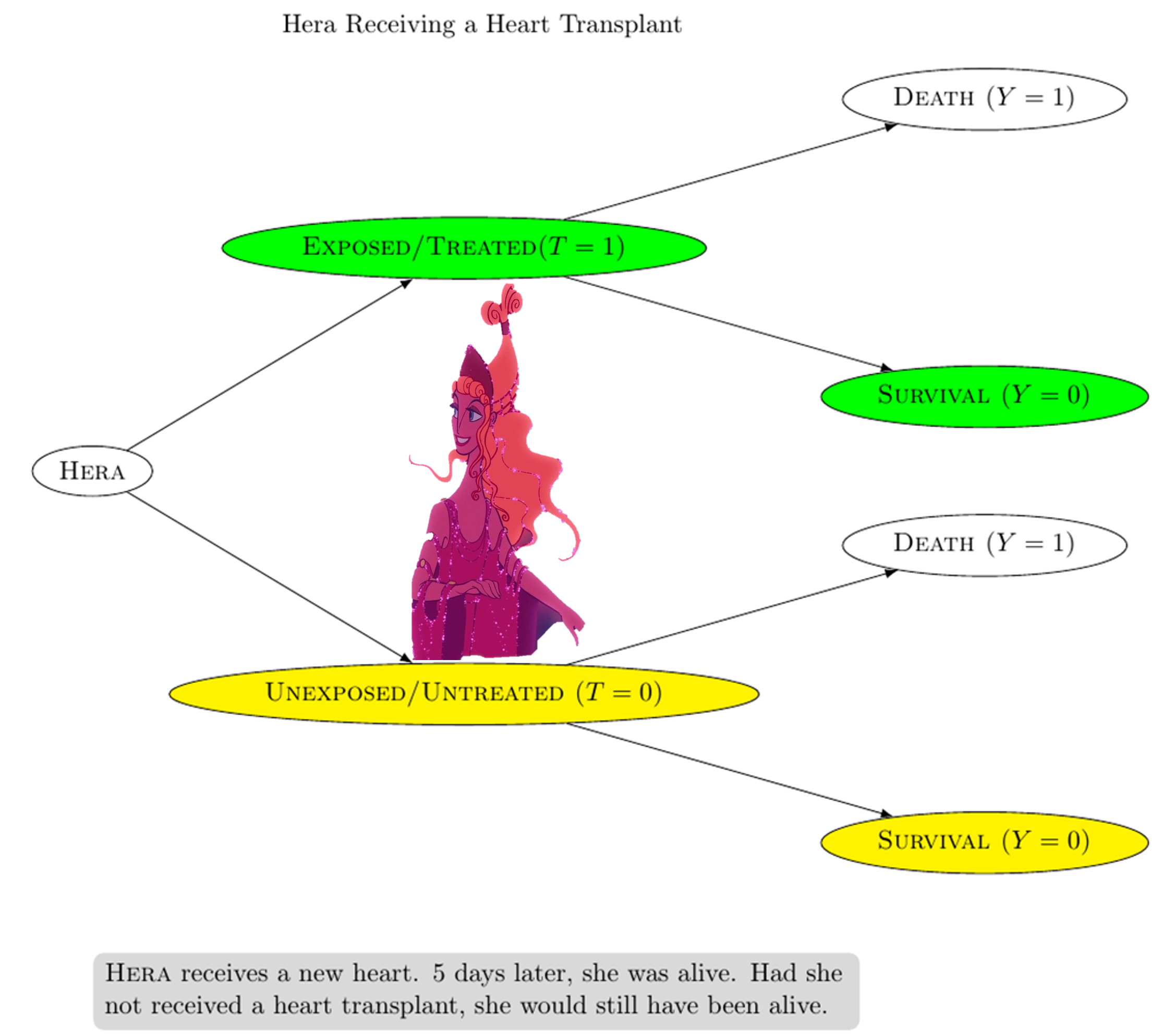

    EXAMPLE 2: Hera (Hernán, 2004)

    In EXAMPLE 2, Hera receives a heart transplant (T = 1)
    5 days later, Hera is still alive (Y = 0)
    Had Hera not received a heart transplant, she would still have been alive (i.e. YT = 0 = 0)

    From EXAMPLE 1 and EXAMPLE 2:
    The actual outcome for Zeus is death (Y = 1) and the counterfactual outcome for Zeus is survival (YT = 0 = 0)
    The actual outcome for Hera is survival (Y = 0) and the counterfactual outcome for Hera is survival (YT = 0 = 0)
    If the two outcomes (actual and counterfactual) differ, then we say that the treatment T has a causal effect on the healthcare outcome Y
    Otherwise, T has no causal effect on the healthcare outcome

    ∴ CONCLUSION 1: The heart transplant caused Zeus' death
    ∴ CONCLUSION 2: The heart transplant had no causal effect on Hera's survival

    Reasoning in terms of counterfactuals provides the basis of causal inference
    Compare with the counterfactual theory of causation
    Well-defined counterfactuals are necessary for meaningful causal inference (Robin & Greenland, 2000)


    Pre-modelling Assumptions
    Suppose that we conduct a 20-person study about the effectiveness of a treatment
    This 20-person study would be too small for us to reach any definite conclusions
    Random fluctuations arising from sampling variability could explain almost anything

    Nonetheless, we could assume that each individual in our population represents 1 billion individuals who are identical to him or her
    ∴ We would end up with a super-population of 20 billion individuals

    Super-population


    ASSUMPTION 1 (Pre-modelling): Individual counterfactual outcomes are deterministic
    We could imagine a scenario in which the counterfactual outcomes are stochastic rather than deterministic w.r.t. an individual
    Perhaps this individual's probability of dying under treatment (0.9) and under no treatment (0.1) are neither zero nor 1
    Nonetheless, our statistical estimates and confidence intervals for causal effects in the super-population are identical, irrespective of whether the world is stochastic (quantum) or deterministic (classical) at the level of individuals

    ASSUMPTION 2 (Pre-modelling): No interference — also known as 'no interference between units' (Cox, 1958) or the 'stable-unit-treatment-value assumption (SUTVA)' (Rubin, 1980)
    An individual's counterfactual outcome under a certain treatment value does not depend on the treatment values of other individuals
    ASSUMPTION 2 would be less feasible in studies where interference between individuals is common (e.g. studies dealing with contagious agents)

    ASSUMPTION 3 (Pre-modelling): Mortality
    Death is delayed, not prevented, by the treatment


    Modelling Assumptions

    Image source: Eric Sucar
    ASSUMPTION 1 (Modelling): Consistency
    In the actual world, Zeus was treated (T = 1)
    According to ASSUMPTION 1, Zeus' counterfactual outcome under treatment (YT = 1 = 1) is equal to his observed outcome Y = 1
    More generally, Yt = Y for every individual with T = t, where t corresponds to an individual's observed treatment value

    The two main COMPONENTS of ASSUMPTION 1 are:
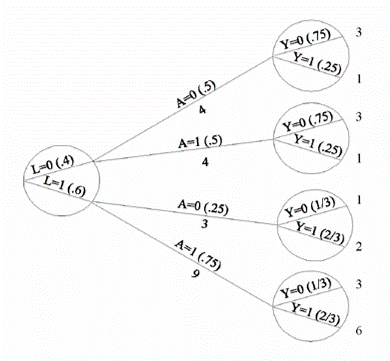
    1. COMPONENT 1: A precise definition of the counterfactual outcome Yt in terms of a specification of the superscript t;
    2. COMPONENT 2: A connection of the counterfactual outcomes to the observed outcomes


    ASSUMPTION 2 (Modelling): Exchangeability
    Exchangeability means that the actual treatment and the counterfactual outcome are independent
    Exchangeability is defined as the independence between the counterfactual outcome YT and the observed treatment T
    When the treated and untreated are exchangeable, we say that the treatment is exogenous

    Formally:
    YT ⫫ T
    NOTE: Exchangeability does not imply independence between the observed outcome and the observed treatment
    YT ⫫ T is mathematically distinct from Y ⫫ T

    Conditional exchangeability:
    YT ⫫ T | L, where L denotes the measured covariates (e.g. L = 1 for patients in a critical condition and L = 0 for patients in a non-critical condition)
    If YT ⫫ T | L, then the treated and untreated are conditionally exchangeable within the levels of variable L
    If YT ⫫ T | L, then the conditional probability of receiving every value of treatment depends only on the measured covariates L


    ASSUMPTION 3 (Modelling): Positivity — also known as the 'experimental treatment assumption'
    The probability of receiving every value of treatment, conditional on L, is greater than zero
    ∴ Under ASSUMPTION 3, there are patients at all levels of treatment (e.g. T = 0, T = 10 in every level of L (e.g. L = 0, L = 1)

    Formally:
    P(T = t|L = l) > 0 for all values of l, with P(L = l) ≠ 0 in the population of interest

    If doctors always transplant a heart (T = 1) to individuals in a critical condition (L = 1), then ASSUMPTION 3 would not hold
    P(T = 0|L = 1) = 0

    ASSUMPTION 1 (Consistency), ASSUMPTION 2 (Exchangeability), and ASSUMPTION 3 (Positivity) are jointly referred to as the identifiability conditions or assumptions



    Randomized experiments


    Observational studies

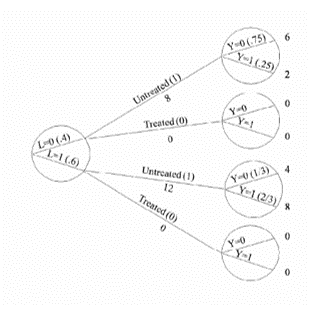
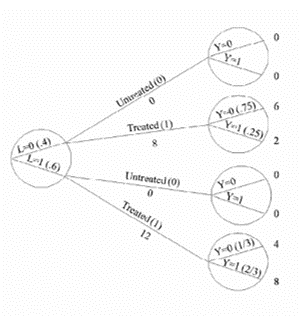
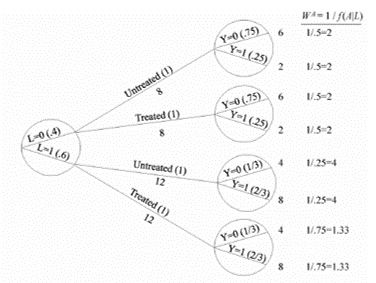
    Randomized experiments are the gold standard and real-world data can be used for causal inference if we conduct randomized experiments
    The randomized assignment of treatment leads to exchangeability
    In a marginally randomized experiment, we use a single unconditional marginal randomization probability
    Randomized controlled trials (RCTs) are supported by Fisher's (1925) theory of experimental design
    EXAMPLE 1: We may flip a single coin to determine whether to assign treatment to each individual
    EXAMPLE 2: We may randomly select 65 patients for treatment
    However, it is often infeasible or impossible to conduct marginally randomized experiments

    A conditionally randomized experiment is a combination of two or more separately marginally randomized experiments
    EXAMPLE 1: A conditionally randomized experiment may be constituted by a combination of two experiments E1 and E2
    E1 is conducted w.r.t. the subset of individuals in critical condition (L = 1)
    E2 is conducted w.r.t. the subset of individuals in non-critical condition (L = 0)
    ∴ In the subset of individuals in critical condition (L = 1), the treated and untreated are exchangeable
    ∴ In the subset of individuals in non-critical condition (L = 0), the treated and untreated are exchangeable


    Observational studies are less convincing because they lack randomized treatment assignment
    However, causal inference from observational data is more plausible if we have grounds for regarding an observational study as a conditionally randomized experiment
    Recall how ASSUMPTION 1 (Consistency), ASSUMPTION 2 (Exchangeability), and ASSUMPTION 3 (Positivity) constitute the identifiability conditions
    If the identifiability conditions (viz. ASSUMPTIONS 1-3) hold, then we can maintain an analogy between observational study and conditionally randomized experiments
    This will allow us to identify causal effects from observational data
    However, whenever any of the identifiablity conditions does not hold, the analogy between observational study and conditionally randomized experiments breaks down (Hernán & Robins, 2020)


    Associational & causal measures

    Associational & Causal Measures

    Type

    Measure

    Formula

    Associational


    Associational risk difference


    P(Y = 1|T = 1) − P(Y = 1|T = 0)


    Associational risk ratio

    P(Y = 1|T = 1)
    P(Y = 1|T = 0)

    Associational odds ratio

    P(Y = 1|T = 1) ÷ P(Y = 0|T = 1)
    P(Y = 1|T = 0) ÷ P(Y = 0|T = 0)

    Causal


    Causal risk difference


    P(YT = 1 = 1) − P(YT = 0 = 1)

    NOTE: The causal risk difference is the average of the individual causal risk differences

    EXAMPLE:
    Suppose that there is a population of 100 million patients
    20 million will die within 5 years if treated (T = 1)
    70 million will die within 5 years if untreated (T = 0)
    ∴ The causal risk difference
    = P(YT = 1 = 1) − P(YT = 0 = 1)
    = 0.2 − 0.7
    = −0.5
    ∴ If one treats all 100 million patients, there will be 50 million fewer deaths
    ∴ (Alternatively) One needs to treat 2 patients to save 1 life


    The number needed to treat (NNT) refers to the average number of individuals who need to receive treatment (T = 1) to reduce the number of mortalities (Y = 1) by one (Laupacis, Sackett, & Roberts, 1988)
    The NNT is equal to the reciprocal of the absolute value of the causal risk difference

    Mathematical formula for NNT:
    −1
    P(YT = 1 = 1) − P(YT = 0 = 1)

    Causal risk ratio

    P(YT = 1 = 1)
    P(YT = 0 = 1)

    Causal odds ratio

    P(YT = 1 = 1) ÷ P(YT = 1 = 0)
    P(YT = 0 = 1) ÷ P(YT = 0 = 0)



    Inverse probability weighting

    Inverse probability weighting (Hernán & Robins, 2020)

    Graph

    Description

    GRAPH 1
    GRAPH 1 is an example of a fully randomized causally interpreted structure tree graph (FRCISTG) (Robins, 1986, 1987)

    There are 20 individuals in this population
    They start at the left of GRAPH 1 and progress over time toward the right
    12 individuals were in a critical condition (L = 1)
    8 individuals were in a non-critical condition (L = 0)
    Of these 8 individuals, 4 were treated (A = 1) and 4 were untreated (A = 0)
    Of the 4 individuals in the branch (L = 0, A = 0), 3 survived (Y = 0) and one died (Y = 1)
      ⋮
    P(L = 0) = 8⁄20 = 0.4
    P(L = 1) = 12⁄20 = 0.6
    P(Y = 0|L = 0, A = 0) = ¾

    NOTE: A or T is traditionally used to denote an action, intervention, or treatment

    GRAPH 2
    GRAPH 2 shows the entire population, had everyone remained untreated (A = 0)

    From GRAPH 1:
    4 out of 8 individuals in a non-critical condition (L = 0) were untreated and 1 died
    ∴ If all 8 individuals with L = 0 remained untreated, then 2 (or 1 × 2) would have died
    3 out of 12 individuals in a critical condition (L = 1) were untreated and 2 died
    ∴ If all 12 individuals with L = 1 remained untreated, then 8 (or 2 × 4) would have died
    ∴ If all 20 individuals (L = 0, L = 1) remained untreated, then 10 (or 2 + 8) would have died

    GRAPH 3
    GRAPH 3 shows the entire population, had everyone been treated (A = 1)
    The simulations in GRAPHS 2 and 3 are correct under conditional exchangeability and can be pooled together to create a pseudo-population
    In this pseudo-population, every individual appears as a treated (A = 1) and as an untreated (A = 0) individual
    ∴ The pseudo-population is twice as large as the original population

    From GRAPH 2:
    P(YT = 0 = 1) = 10⁄20 = 0.5 — (1)

    From GRAPH 3:
    P(YT = 1 = 1) = 10⁄20 = 0.5 — (2)
    ∴ Causal risk ratio = 0.5⁄0.5 = 1 — from (1) & (2)

    GRAPH 4
    Here is the inverse probability (IP) weighting method:
    The 4 untreated individuals (A = 0) with L = 0 are used to create 8 members of the pseudo-population (i.e. if all individuals with L = 0 remained untreated)
    ∴ Each of them receives a weight of 2 (or 8⁄4)

    The 9 treated individuals (A = 1) with L = 1 are used to create 12 members of the pseudo-population (i.e. if all individuals with L = 1 were treated)
    ∴ Each of them receives a weight of 1.33 (or 12⁄9)
      ⋮

    Overall, the pseudo-population is created by weighting each individual in the population by the inverse of the conditional probability of receiving the treatment level that she indeed received
    GRAPH 4 shows the IP weights
     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .