• Back to Profile
    •  

     


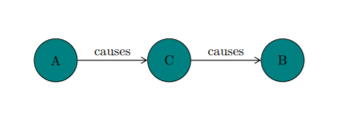
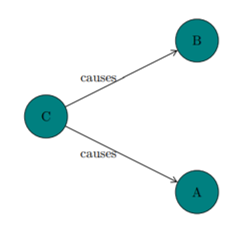
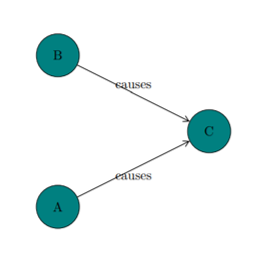
    When one particular species of event has always … been conjoined with another,
    we make no longer any scruple of foretelling one upon the appearance of the other,
    and of employing that reasoning, which can alone assure us of any matter of fact or existence.
    We then call the one object, Cause; the other, Effect.
    - David Hume's (1748, §7) An Enquiry Concerning Human Understanding

     

     

     

     

    Pearl Causal Model

    Graph Theory

    Judea Pearl


    Peter Spirtes

    1. The Pearl Causal Model relies on a graphical approach to causality (Spirtes et al, 2000, Pearl, 2000, 2009)
    2. The intellectual background of the Pearl Causal Model includes the graph-theoretical work of Lauritzen, Speed, & Vijayam (1978), Darroch, Lauritzen, & Speed (1980), and Wermuth & Lauritzen (1983)


    1. In graph theory, a graph G = 〈 V, E 〉, where V is a set of vertices and E is a set of edges
    2. The members of E are pairs of vertices: these pairs are ordered in a directed graph and unordered in an undirected graph
    3. The directed edge A → B is represented by the ordered pair 〈 A, B 〉
    4. A path is any consecutive sequence of edges, regardless of directionality
    5. For a directed path from A to B, A is the source of the path and B is the sink of the path

    7. If there is a directed edge from A to B, then:
      1. A is the parent of B
      2. B is the child of A

    9. Parents(V) denotes the set of all parents of vertices in V
    10. Children(V) denotes the set of all children of vertices in V
    11. The indegree of a vertex V1 is the number of parents of V1
    12. The outdegree of a vertex V1 is the number of children of V1
    13. The degree of a vertex V1 is the number of vertices adjacent to V1
    14. The ancestor of a vertex V1 is any vertex Vi such that there is a directed path from Vi to V1
    15. The descendant of a vertex V1 is any vertex Vi such that there is a directed path from V1 to Vi

    GRAPH 1

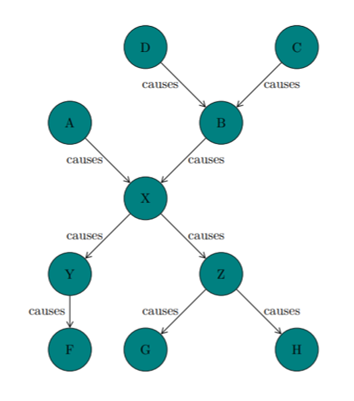
    Relative to GRAPH 1:
    The parents of X are A and B
    The ancestors of X are D, C, A, and B
    The children of X are Y and Z
    The descendants of X are Y, Z, F, G, and H
    The indegree of X is 2
    The outdegree of X is 2
    The degree of X is 4



    Types of Paths

    Path

    Description




    Direct causality
    A ⫫ B




    Indirect causality
    A ⫫ B
    A ⫫ B|C

    There may be overcontrol bias when one intercepts or blocks a causal pathway





    Fork with C as the common cause or confounder
    A ⫫ B
    A ⫫ B|C

    There may be confounding bias when one fails to condition on a common cause or confounder





    Inverted fork with C as the common effect or collider
    A ⫫ B
    A ⫫ B|C

    There may be endogenous selection bias when one mistakenly conditions on a common effect or collider



    D-separation




    The rules for d-separation (Pearl, 1988):
    RULE 1 for d-separation ('d' stands for 'directional'): X and Y are d-connected if there is an unblocked path between X and Y
    An unblocked path is a path that can be traced without meeting with any colliders


    EXAMPLE 1

    In EXAMPLE 1:
    There is a collider at T
    The path X-R-S-T is unblocked
    ∴ X and R, X and S, X and T, R and S, R and T, and S and T are d-connected
    The path T-U-V-Y is also unblocked
    ∴ T and U, T and V, T and Y, U and V, U and Y, and V and Y are also d-connected
    However, X and Y, X and V, S and U, etc are d-separated: no path can be traced between them without meeting the collider at T

    RULE 2 for d-separation: X and Y are d-connected, conditioned on a set Z of nodes, if there is a collider-free path between X and Y that does not traverse any members of Z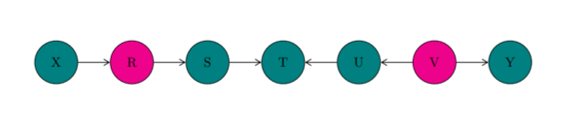


    EXAMPLE 2

    In EXAMPLE 2:
    Let Z be the set { R, V }
    According to RULE 2:
    X and S are d-separated: the path X-R-S is blocked by Z
    U and Y are d-separated: the path U-V-Y is blocked by Z
    S and U are d-separated: the path S-T-U is not collider-free
    Although T is not in Z, the path S-T-U is still blocked since T is a collider (RULE 1)

    RULE 3 for d-separation: If a collider is a member of the conditioning set Z or the collider has a descendant in Z, then it no longer blocks any path that traces this collider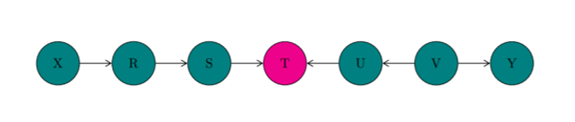

    EXAMPLE 3

    In EXAMPLE 3:
    Let Z be the set { T }
    According to RULE 3:
    X and Y, X and V, S and U, etc are now d-connected, since the collider T is a member of the conditioning set Z (compare with EXAMPLE 1)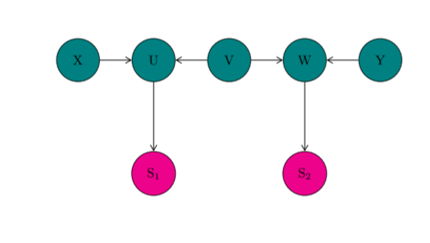
    EXAMPLE 4

    In EXAMPLE 4:
    Let Z be the set { S1, S2 }
    According to RULE 3:
    The collider at U has a descendant S1 in the conditioning set Z and the link at U is unblocked
    The collider at W has a descendant S2 in the conditioning set Z and the link at W is unblocked
    ∴ We now have a collider-free path between X and Y (viz. X-U-V-W-Y) that does not traverse any members of the conditioning set Z


    There are 3 blocking criteria:
    1. CRITERION 1: Conditioning on a non-collider blocks a path
    2. CRITERION 2: Conditioning on a collider or a descendant of a collider unblocks a path
    3. CRITERION 3: Not conditioning on a collider leaves a path naturally blocked


    A d-separated (or blocked) path does not transmit association
    A d-connected (or unblocked) path may transmit association

    DAGs & Bayesian Networks

    Massive Bayesian network
    The Pearl Causal Model takes a set of data and produces a directed acyclic graph (DAG)
    A DAG is:
    1. Directed — Each directed edge is single-headed, expressing a causal statement
      'A → B' denotes that A directly causes B
    2. Acyclic — There are no directed cycles
      'A → B → C → A' is impossible
    3. Graphical — DAGs employ the mathematical structure of graphs:
      1. Vertices or nodes stand for variables;
      2. Directed edges or arrows stand for possible direct causal effects;
      3. Missing arrows encode assumptions about absent direct causal effects


    A DAG is also called a Bayesian network (BN)
    The DAG represents the causal structure of the system
    Conditional dependence relations between variables are represented as edges between vertices in the graph
    The main idea behind the Pearl Causal Model is to find a graph or set of graphs that best explain the data


    There are two primary METHODS for inferring BNs from the data:
    METHOD 1: Assign scores to graphs and search over the set of possible graphs, while attempting to maximize a particular scoring function
    An initial graph is generated in METHOD 1 and the search space is explored by altering this graph

    METHOD 2: Start with an undirected, fully connected graph and use repeated conditional independence tests to remove and orient edges in the graph
    After the edges are removed, the remaining ones are directed from cause to effect

    Example of a DBN

    Image source: Wikipedia

    Dynamic Bayesian networks (DBNs) use BNs to show how variables influence each other across time (Friedman et al, 1998, Murphy, 2002)
    1. STEP 1: There is generally an initial Bayesian network (BN) depicting connections between variables at some time t;
    2. STEP 2: There is then a set of BNs showing the system at t + 1, t + 2, etc

    Axioms

    Axioms
    AXIOM 1: Causal Markov Condition (CMC)
    A directed acyclic graph (DAG) G over V and a probability distribution P(V) satisfies the CMC iff for every W in V, W is independent of its non-effects, given its parents

    (Alternatively) Given any disjoint sets A, B, and C of variables, if A is d-separated from B conditional on C, then A is statistically independent of B given C
    See Pearl (1988) for proof

    Formally:
    W ⫫ { V \ Descendants(W) ∪ Parents(W) }|Parents(W)

    EXAMPLE 5

    In EXAMPLE 5:
    The CMC entails the following conditional independence relations:
    A ⫫ B
    D ⫫ { A, B }|C

    AXIOM 2: Causal Faithfulness Condition (CFC)
    Given any graph, the CMC (or AXIOM 1) determines a set of independence relations
    However, a probability distribution P on a graph G that satisfies the CMC may include other independence relations besides those entailed by the CMC

    Recall the birth control pill EXAMPLE (Hesslow, 1976, Cartwright, 1989):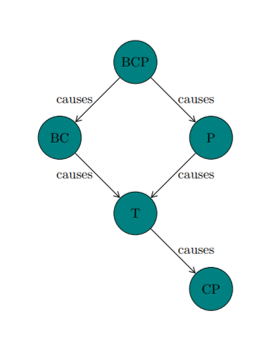


    BCP (birth control pills) and T (thrombosis) might be independent in the probability distribution satisfying the CMC for this graph, even though the graph does not entail their independence

    ∴ If all and only those conditional independence relations true in P are entailed by the CMC applied to G, then we say that P and G are faithful to one another
    (Alternatively) Given any disjoint sets A, B, and C of variables, if A is statistically independent of B given C, then A is d-separated from B conditional on C


    AXIOM 3: Causal Sufficiency
    A set V of variables is causally sufficient for a population iff in the population every common cause of any 2 or more variables in V is in V
    According to AXIOM 3, there are no hidden common causes


    Intervention & the Do-calculus

    Intervention


    Do-calculus
    EXAMPLE:
    Here is the DAG for the relationship between temperature, ice cream sales, and crime rates:

    (Pearl, Glymour, & Jewell, 2016)

    X denotes ice cream sales
    Y denotes crime rates
    Z denotes the temperature
    UX, UY, and UZ denote the error terms for X, Y, and Z (i.e. the effects of exogenous variables not included in the causal model

    Suppose that we intervene on the value of ice cream sales (X)
    We might fix the value of X to a low value (e.g. by shutting down all ice cream shops)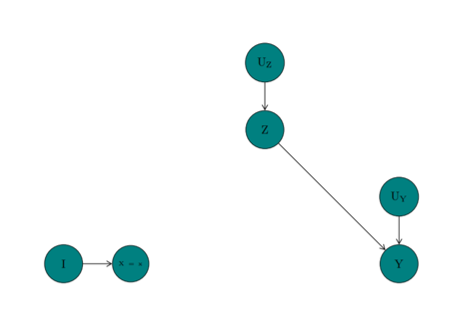


    When we intervene on X:
    1. We fix the value of X to a certain value (i.e. X = x);
    2. We curtail the natural tendency of X to vary in response to the other variables Y and Z


    5. ∴ The intervention I breaks all other directed edges or arrows previously directed into X (viz. Z → X, UX → X)
    6. These directed edges are replaced by a single directed edge from the intervention variable I to X
    7. Y is now totally uncorrelated with X, since X is no longer associated with Z



    1. The removal of all edges directed into X has been described as 'surgery'
    2. The tacit assumption here is that intervention or surgery has no side effects
    3. This has been described as the arrow-breaking conception of interventions (Pearl, 2000, Spirtes et al, 2000)

    According to the do-calculus:
    Given 2 disjoint sets of variables X and Y, the causal effect of X on Y is a function from X to the space of probability distributions on Y
    The causal effect of X on Y is denoted as 'P(y | do(x))' in the do-calculus
    For each realization x of X, P(y | do(x)) gives the probability of Y = y induced by deleting from the model all equations corresponding to variables in X and substituting X = x in the remaining equations The graph corresponding to the reduced set of equations is the subgraph from which all directed edges entering X have been pruned by surgery


    Where x1, …, xn denote variables in a BN:
    P(x1, …, xn) = ∏ P(xi|Parents(xi)

    According to Cochrane's EXAMPLE (Wainer, 1989):
    Soil fumigants (X) are being used to increase oat crop yields (Y) by controlling the eelworm population (Z)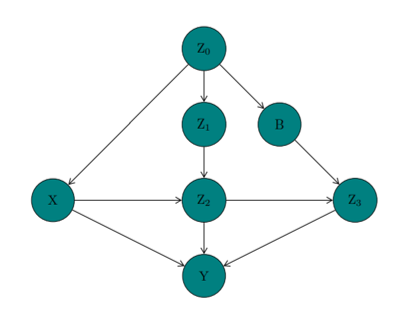

    Cochrane's EXAMPLE

    X denotes the soil fumigants
    Y denotes the oat crop yields
    Z denotes the eelworm population: Z0 denotes last year's eelworm population, Z1 denotes the quantity of eelworm population before treatment, Z2 denotes the quantity of eelworm population after treatment, and Z3 denotes the quantity of eelworm population at the end of the season
    B denotes the population of birds and other predators

    From P(x1, …, xn) = ∏ P(xi|Parents(xi), we get:
    P(z0, x, z1, b, z2, z3, y) = P(z0)P(x|z0)P(z1|z0)P(b|z0) × P(z2|x, z1)P(z3|z2, b)P(y|x, z2, z3)

    With the intervention do(X = x′):
    P(z0, z1, b, z2, z3, y|do(X = x′)) = P(z0)P(z1|z0)P(b|z0) × P(z2|x′, z1)P(z3|z2, b)P(y|x′, z2, z3)
     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .