• Back to Profile
    •  

     


    I propose to consider the question, 'Can machines think?'
    This should begin with definitions of the meaning of the terms 'machine' and 'think'.
    The definitions might be framed so as to reflect so far as possible the normal use of words,
    but this attitude is dangerous.

    If the meaning of the words 'machine' and 'think' are to be found
    by examining how they are commonly used
    it is difficult to escape the conclusion that the meaning
    and the answer to the question, 'Can machines think?'
    is to be sought in a statistical survey such as a Gallup poll. But this is absurd.
    - A. M. Turing's (1950, p. 433) 'Computing Machinery and Intelligence'

     

     

     

     

    Thinking like a Human


    1. The thinking like a human approach is concerned with understanding the actual workings of human minds
    2. The thinking like a human approach is also known as the cognitive modelling approach
    3. The thinking like a human approach is associated with connectionist AI, ANNs (artificial neural networks), subsymbolic AI, etc


    6. The thinking like a human approach is supported by:
      1. The Subsymbolic Hypothesis or SSH (Smolensky, 1987)
      2. The McCulloch-Pitts Model of the Neuron (McCulloch & Pitts, 1943, 1947)
      3. The Learning Rule of Synaptic Reinforcement (Hebb, 1949)
      4. Backpropagation (Rumelhart, Hinton, & Williams, 1986)


    Paul Smolensky
    Recall the Physical Symbol System Hypothesis or PSSH (Newell & Simon, 1976):

    A physical symbol system has the necessary and sufficient means for intelligent action
    The 2 most important classes of physical symbol systems with which we are acquainted are human beings and computers


    2 classes of physical symbol systems

    If the PSSH is true, then there must exist a complete description of cognitive processing at the symbolic level
    However, no such description exists

    According to the thinking like a human approach:
    To give a full account of mental processes and operations, one must instead invoke processes that lie beneath the symbolic level


    According to the Subsymbolic Hypothesis or SSH (Smolensky, 1987):

    Let an intuitive processor denote a machine that runs programs responsible for behaviour that is not conscious rule application
    A precise and complete formal description of the intuitive processor does not exist


    An intuitive processor


    IMPLICATIONS of the SSH:

    The intuitive processor is a subconceptual connectionist system
    The intuitive processor operates at an intermediate level between the neural level and the symbolic level
    Connectionist systems are much closer to neural networks than symbolic systems



    Warren McCulloch & Walter Pitts
    Recall that the basic units of the thinking rationally approach are propositions, about which persons have propositional attitudes — see Bringsjord's (2008) Logicist Manifesto
    The thinking rationally approach is concerned with the laws of thought, the mind, and its mental operations

    Conversely, the basic units of the thinking like a human approach are neurons
    Neurons are the basic working units of the brain
    The thinking like a human approach is concerned with the brain
    As real neurons are exceedingly complex, the aim of the thinking like a human approach is to model our understanding of neurons in a computationally feasible manner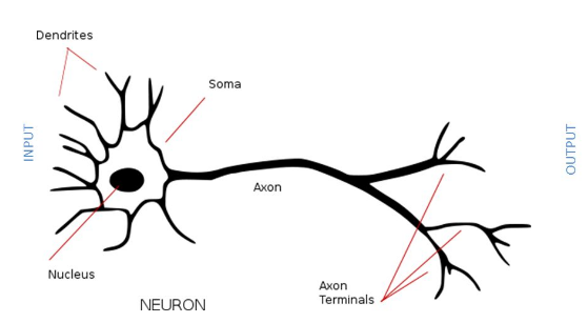



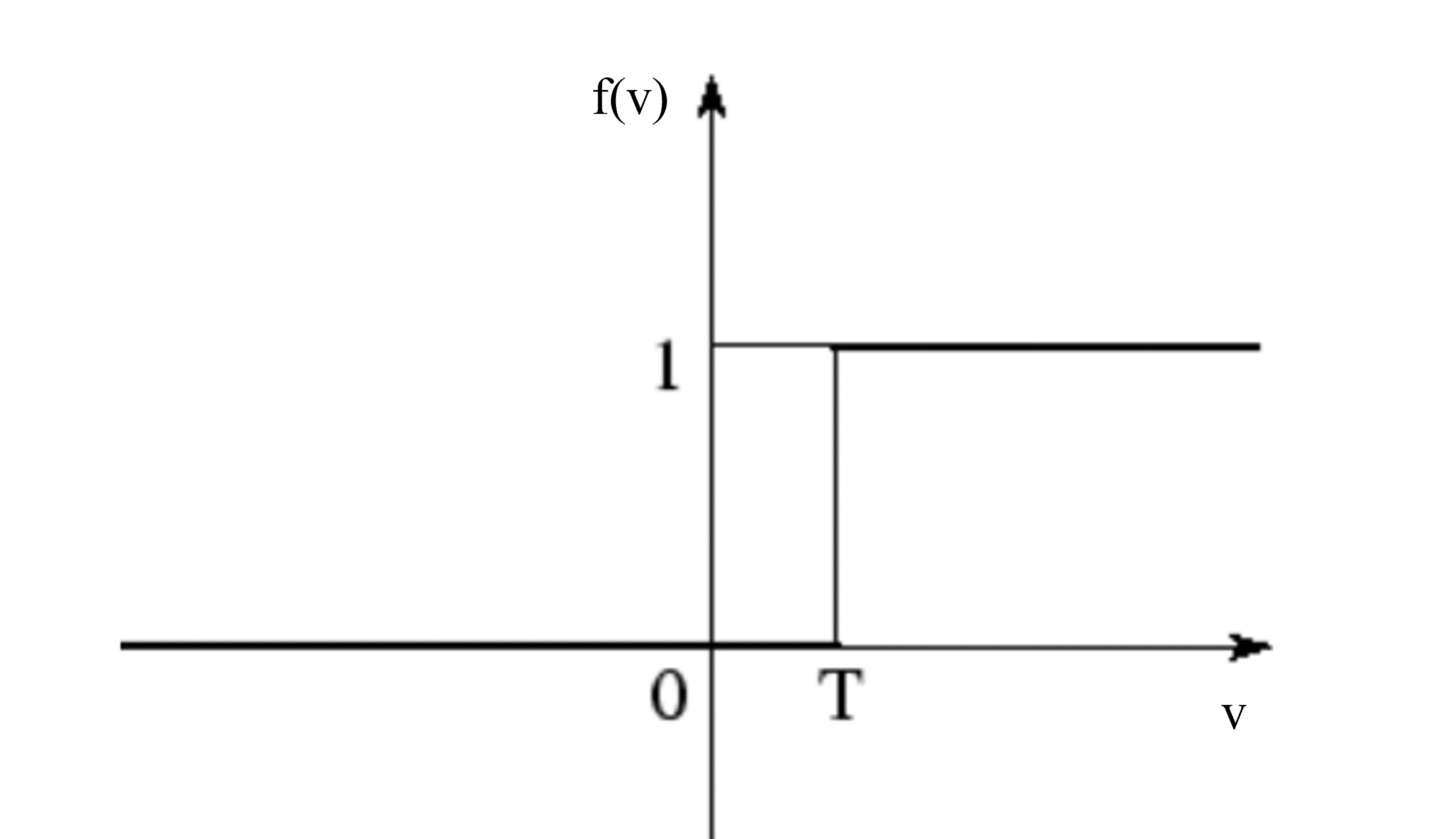
    1. Each neuron or nerve cell is an electrically excitable cell that takes up, processes, and transmits information through electrical and chemical signals

    3. Each neuron has 3 main parts:
      1. PART 1: Dendrites — Electrical and chemical signals are received by the dendrites and brought to the cell body
      2. PART 2: Soma or cell body — Electrical and chemical signals are brought to the cell body
      3. PART 3: Axon — Electrical and chemical signals are conducted away from the cell body by the axon and the axon transmits information to other neurons

    According to the McCulloch-Pitts Model of the Neuron (McCulloch & Pitts, 1943, 1947):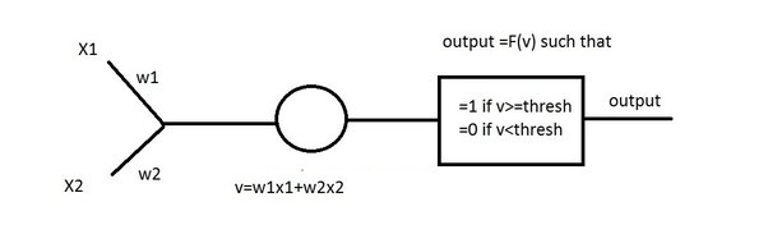


    1. A real neuron is essentially equivalent to a logic gate
    2. x1 and x2 are the inputs
    3. w1 and w2 are the associated weights

    4. v = Σ(xi × wi)


    6. Where T denotes a threshold value, f(v) is a thresholding function that may be characterized as follows:
      1. f(v) = 1 when v ≥ T
      2. Otherwise, f(v) = 0 when v < T

      4. ∴ f(v) may be represented mathematically as a linear step function:


    Donald Hebb
    According to the Learning Rule of Synaptic Reinforcement (Hebb, 1949):
    A synapse is a structure that permits a neuron to transmit an electrical or chemical signal to another neuron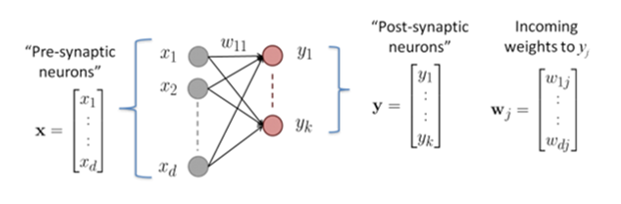


    xi denotes the output of the input (pre-synaptic) cell
    yi denotes the output of the output (post-synaptic) cell
    w11 denotes the synaptic weight from x1 to y1
    More generally, wij denotes the synaptic weight from xi to yj
    Δwij denotes the strength of the change in synaptic weight from xi to yj


    When neuron xi (pre-synaptic) fires, followed by neuron yj (post-synaptic) firing, the synapse between xi and yj is strengthened
    ∴ Δwij will be positive


    Slogan for the Hebbian learning mechanism:
    Neurons that fire together, wire together


    Diagram of perceptron
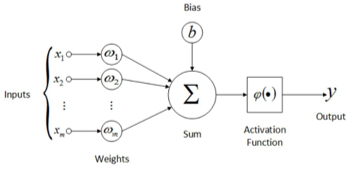
    The perceptron was an algorithm that could learn to associate inputs with outputs (Rosenblatt, 1958, 1962)
    The perceptron incorporated the following:
    1. The McCulloch-Pitts Model of the Neuron (McCulloch & Pitts, 1943, 1947)
    2. The Learning Rule of Synaptic Reinforcement (Hebb, 1949)

    Let the bias of the perceptron be denoted by b
    Let 'x' and 'o' represent patterns with a set of values { x1, x2 }
    Let w1 and w2 denote the associated weights of x1 and x2

    The perceptron could make correct classifications of patterns by virtue of:
    1. A choice of values for w1, w2, and b that classifies all training examples correctly into 'x' or 'o';
    2. The linear separability assumption

    The classes of 'x' and 'o' can be separated by a single line L

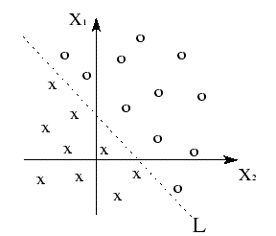
    IMPLICATIONS:
    1. Different values for w1, w2, and b correspond to different lines
    2. Learning the values for w1, w2, and b means varying the direction of the line
    4. If the linear separability assumption holds, then there exists a choice of values for w1, w2, and b that will allow the perceptron to correctly classify all training examples into one of two class (viz. 'x' or 'o')

    Diagram for linear separability (Abu-Mostafa, Magdon-Ismail & Lin, 2012, p. 6)

    Marvin Minsky & Seymour Papert's (1969) Perceptrons: An Introduction to Computational Geometry

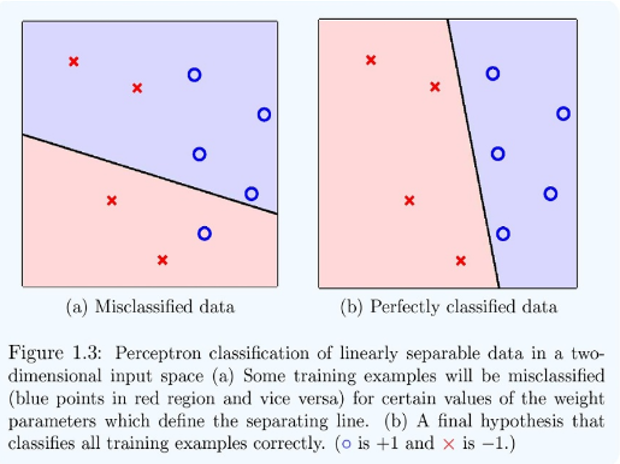
    Argument (Minsky & Papert, 1969):
    1. P1: For any pattern, if the perceptron can correctly classify that pattern, then the linear separability assumption must hold for that pattern.
    2. P2: The linear separability assumption does not hold for all patterns.
    3. C: ∴ The perceptron cannot correctly classify all patterns.

    5. Formally:
    6. P1: ∀x(Cx → Lx), where x denotes a pattern
    7. P2: ∃x(∼Lx)
    8. C: ∴ ∃x(∼Cx)

    IMPLICATIONS of this argument:
    There are some patterns (including extremely simple ones like the XOR logic function) that no perceptron could learn
    This is known as the linear separability problem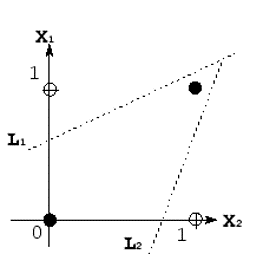


    Let white dots (•) denote the class of x1 ⊻ x2 bearing the truth value of 1/T
    Let black dots (•) denote the class of x1 ⊻ x2 bearing the truth value of 0/F
    The two classes (represented by • and •) cannot be separated by a single line


    David Rumelhart, Geoffrey Hinton, & Ronald Williams
    According to Backpropagation (Rumelhart, Hinton, & Williams, 1986):
    1. The linear separability problem can be overcome
    2. Given a sufficient number of hidden neurons, backpropagation (based on a multi-layered network) could learn increasingly complex decision boundaries


    1. STEP 1: Compare a system's output with the desired output
    2. STEP 2: Successively change the connections in layer after layer of neurons

    Figure of a multi-layered backpropagation network

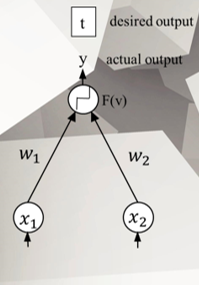
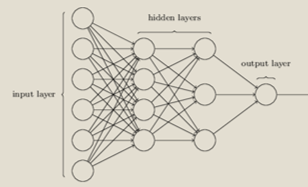
    Defenders of the thinking like a human approach will recommend more complex (e.g. multi-layered) networks and more complex transfer functions (e.g. multi-step as opposed to linear step functions)

     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .