• Back to Profile
    •  

     


    I propose to consider the question, 'Can machines think?'
    This should begin with definitions of the meaning of the terms 'machine' and 'think'.
    The definitions might be framed so as to reflect so far as possible the normal use of words,
    but this attitude is dangerous.

    If the meaning of the words 'machine' and 'think' are to be found
    by examining how they are commonly used
    it is difficult to escape the conclusion that the meaning
    and the answer to the question, 'Can machines think?'
    is to be sought in a statistical survey such as a Gallup poll. But this is absurd.
    - A. M. Turing's (1950, p. 433) 'Computing Machinery and Intelligence'

     

     

     

     

    Thinking Rationally


    1. The thinking rationally approach is concerned with the laws of thought that govern the operations of the mind
    2. The thinking rationally approach is associated with classical AI, GOFAI (good old-fashioned AI), symbolic AI, logic-based AI, knowledge-based AI, etc

    3. The thinking rationally approach is supported by:
      1. The Physical Symbol System Hypothesis or PSSH (Newell & Simon, 1976)
      2. The Heuristic Search Hypothesis or HSH (Newell & Simon, 1976)
      3. The Logicist Manifesto (Bringsjord, 2008)


    Herbert Simon & Allen Newell playing chess
    According to the Physical Symbol System Hypothesis or PSSH (Newell & Simon, 1976):

    A physical symbol system has the necessary and sufficient means for intelligent action
    The 2 most important classes of physical symbol systems with which we are acquainted are human beings and computers


    2 classes of physical symbol systems


    IMPLICATIONS of the PSSH:

    The symbolic behaviour of human beings arises because we have the characteristics of a physical symbol system
    General intelligent action calls for a physical symbol system
    Appropriately programmed computers would be capable of intelligent action
    Intelligent systems (natural or artificial) are effectively equivalent


    Egyptian hieroglyphs


    According to the Heuristic Search Hypothesis or HSH (Newell & Simon, 1976):

    Physical symbol systems solve problems using the processes of heuristic search
    Solutions to a problem are represented as symbol structures
    A physical symbol system exercises its intelligence in problem-solving by searching until the symbol structures of solutions are produced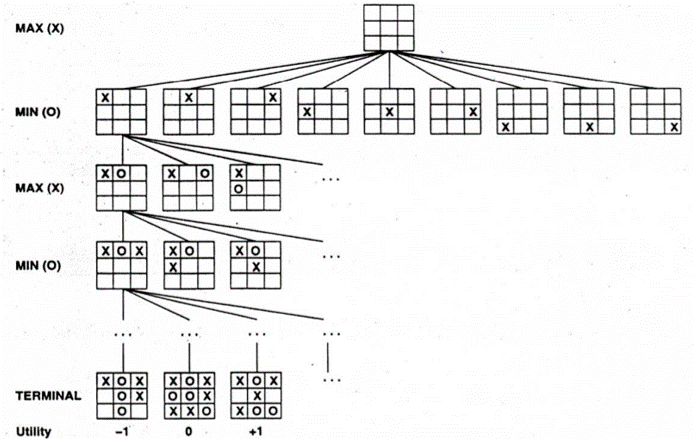


    A partial game tree for Tic-tac-toe


    Selmer Bringsjord
    According to the Logicist Manifesto (Bringsjord, 2008):

    A person is the bearer of propositional attitudes:
    1. X knows that p
    2. X believes that p
    3. X imagines that p
    4. X intends to bring about that p

    The basic units are propositions or declarative statements (denoted by propositional variables p, q, etc) that convey propositional content
    Propositions can carry such values as TRUE, FALSE, PROBABLE, UNKNOWN, etc
    The basic processes over units of inference are the modes of reasoning (viz. deductive, inductive, abductive, analogical, etc)


    Logic-based AI has three attributes:

    1. ATTRIBUTE 1: Logic-based AI is ambitious: it aims to construct artificial persons
    2. ATTRIBUTE 2: Logic-based AI is person-oriented: it formalizes one of the distinctive features of persons (viz. their being bearers of propositional attitudes)
    3. ATTRIBUTE 3: Logic-based AI is top-down


    Alfred North Whitehead & Bertrand Russell's (1910, 1912, 1913) Principia Mathematica
    EXAMPLE 1: Logic Theorist or LT (Newell, Shaw, & Simon, 1957)
    LT is a logical theorem-proving program capable of providing proofs in propositional logic LT managed to prove 38 of the first 52 theorems in Whitehead & Russell's (1910, 1912, 1913) Principia Mathematica

    Input

    Processing

    Output
    AXIOMS:
    1. A1.2: ⊦ (p ∨ p) → p
    2. A1.3: ⊦ p → (p ∨ q)
    3. A1.4: ⊦ (p ∨ q) → (q ∨ p)
    4. A1.5: ⊦ (p ∨ (q ∨ r)) → (q ∨ (p ∨ r))
    5. A1.6: ⊦ (p ∨ q) → ((r ∨ p) → (r ∨ q))

    DEFINITIONS:
    1. D1.01 (material conditional): (p → q) ⟷ (∼p ∨ q)
    2. D3.01 (conjunction): (p ∧ q) ⟷ ∼(∼p ∨ ∼q)
    3. D4.01 (material biconditional): (p ⟷ q) ⟷ ((p → q) ∧ (q → p))

    RULES OF INFERENCE:
    1. R1 (Rule of substitution): Any expression may be substituted for any variable in any theorem, provided the substitution is made throughout the theorem wherever that variable appears

    3. R2 (Rule of replacement): A logical connective can be replaced by its definition and vice versa

    5. R3 (Rule of detachment (modus ponens)): If 'A' and 'A → B' are theorems, then 'B' is a theorem
    LT relies on AXIOMS, DEFINITIONS, RULES OF INFERENCE, and previous steps in an uncompleted PROOF to come up with and complete a PROOF for the THEOREM


    LT offers a PROOF of the THEOREM within a finite amount of time


    THEOREM: (p → q) → (∼q → ∼p))


    PROOF:
    1. Relations p:0, q:0 (i.e. propositional variables are 0-ary relations)
    2. assume p → q
    3.   assume ∼q
    4.     suppose-absurd p
    5.       begin
    6.         modus-ponens p → q, p;
    7.         absurd q, ∼q
    8.       end

    LT was able to provide a more elegant proof for a logical theorem (THEOREM 2.85) than the one found in Whitehead & Russell (1910, 1912, 1913)
    THEOREM 2.85: ((p ∨ q) → (p ∨ r)) → (p ∨ (q → r))

    Simon claimed to have solved the mind-body problem with LT
    However, the editors of the Journal of Symbolic Logic rejected a paper co-authored by Newell, Simon, and LT



    John McCarthy
    EXAMPLE 2: Advice Taker or AT (McCarthy, 1959)
    AT is program designed by John McCarthy and Marvin Minsky for solving problems by manipulating sentences in a formal language
    AT will draw immediate conclusions from a premise set
    The conclusions will be either declarative or imperative sentences

    Input

    Processing

    Output
    GOAL:
    1. P13: want(at(I, airport)) — I want to be at the airport

    DEFINITIONS:
    1. P6: transitive(at) — 'at' (a 2-place predicate) is transitive
    2. P7: transitive(u) → (u(x, y), u(y, z) → u(x, z)) — definition of transitivity

    4. P14: (x → can(y)), (did(y) → z) → canachult(x, y, z) — 'canachult' is a 3-place predicate: in a situation to which x applies, the action y can be performed and ultimately brings about a situation to which z applies
    5. P15: canachult(x, y, z), canachult (z, u, v) → canachult(x, prog(y, u), v) — where 'prog (y, u)' (first carry out action y, then action u) is a 2-place predicate, 'canachult' is semi-transitive

    FACTS:
    1. P1: at(I, desk) — I am at my desk
    2. P2: at(desk, home) — My desk is at home
    3. P3: at(car, home) — The car is at home
    4. P4: at(home, county) — My home is at the county
    5. P5: at(airport, county) — The airport is at the county
    6. P10: walkable(home) — Home is walkable
    7. P11: drivable(county) — The county is drivable

    RULES:
    1. P8: walkable(x), at(y, x), at(z, x), at(I, y) → can(go(y, z, walking)) — If x is walkable, y is at x, z is at x, and I am at y, then I can go from y to z by walking, where 'go(y, z, walking)' (go from point y to point z by the action of walking) is a 3-place predicate

    3. P9: drivable(x), at(y, x), at(z, x), at(car, y), at(I, car) → can(go(y, z, driving)) — If x is drivable, y is at x, z is at x, the car is at y, and I am at the car, then I can go from y to z by driving

    5. P12: did(go(x, y, z)) → at(I, y) — If I did go from x to y by action z, then I am at y

    7. P16: x, canachult(x, prog(y, z),w), want(w) → do(y) — If x, the actions y and then z can be performed in a situation to which x applies to bring about a situation to which w applies, and I want w, then I perform action y


    		 Given the GOAL, DEFINITIONS, FACTS, and RULES, AT will deduce an ARGUMENT to solve a PROBLEM AT offers an ARGUMENT in order to SOLVE the PROBLEM

    PROBLEM:
    I am seated at my desk at home and I wish to go to the airport. My car is at my home too.

    Q: What do I do?




    ARGUMENT:
    1. 1. at(I, desk) → can(go(desk, car, walking)) — from P1, P2, P3, P8, P10
    2. 2. at(I, car) → can(go(home, airport, driving)) — from P3, P4, P5, P9, P11
    3. 3. did(go(desk, car walking)) → at(I, car) — from P12
    4. 4. did(go(home, airport, driving)) → at(I, airport) — from P12
    5. 5. canachult(at(I, desk), go(desk, car, walking), at(I, car)) — from 1., 3., P14
    6. 6. canachult(at(I, car), go(home, airport, driving), at(I, airport)) — from 2., 4., P14
    7. 7. canachult(at(I, desk), prog(go(desk, car, walking), go(home, airport, driving)), at(I, airport)) — from 5., 6., P15
    8. 8. do(go(desk, car, walking)) — from P1, 7., P13, P16

    10. 8. initiates action
    11. The SOLUTION to the PROBLEM is to go from the desk to the car by walking
    12. Thereafter, I can drive the car to the airport
     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .