• Back to Profile
    •  

     

     

     

     

     



    Go & chess


    The drosophila


    1. EXAMPLE of an evaluation function (Shannon, 1950):
    2. Let K, Q, R, B, N, and P denote the number of White kings, queens, rooks, bishops, knights and pawns on the board
    3. Let K′, Q′, R′, B′, N′, and P′ denote the number of Black kings, queens, rooks, bishops, knights and pawns on the board
    4. Let D, S, and I denote the double, backward or isolated White pawns
    5. Let D′, S′, and I′ denote the double, backward or isolated Black pawns

    7. Function f = 200(K - K′) + 9(Q - Q′) + 5(R - R′) + 3(B - B′ + N - N′) + (P - P′) – 0.5(D - D′ + S - S′ + I - I′)


    1. The drosophila (or the humble fruit fly) is a good model organism in biology, neuroscience, and genetics
    2. Chess has been described by Alexander Kronrod as the drosophila of AI research


    5. How do we design an AI system to play a skilful (i.e. human expert-level) game of chess?


    8. RESPONSE 1: We could rely on a set of principles
      1. PRINCIPLE 1: The player with greater mobility has the better game
      2. PRINCIPLE 2: Different PRINCIPLES apply in different phases (e.g. opening, middle game, endgame) of the game
      3.        ⋮

    10. RESPONSE 2: We could rely on an evaluation function

    12. RESPONSE 3: We could rely on a minimax algorithm




    Hover over here to see js code snippet for the minimax algorithm


    Go

    1. Go (围棋 or weiqi) is a 2-player sequential zero-sum game with perfect information
    2. The aim of Go is for each player to surround more territory than the opponent



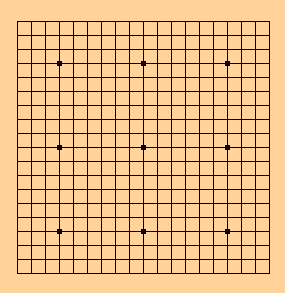    Go board
    1. There are 19 vertical lines and 19 horizontal lines on the Go board
    2. This yields 361 (or 192) points or intersections
    3. 9 points on the board are dotted and called star points
    4. The point in the centre is called the central star

    The rules of Go
    1. P1 (Black) takes the black stones and makes the first move
    2. P2 (White) takes the white stones and makes the next move
    3. P1 (Black) and P2 (White) take turns to move and only one stone can be played per move

    5. A stone on the Go board has 2-4 adjacent intersections
    6. Whichever of these intersections is/are unoccupied would be called liberties
    7. Stones adjacent to other stones of the same colour form a unit and their liberties are counted together
    8. When all the liberties of a stone or group of stones have been taken by the opposite colour, those stones cannot remain on the board
    9. The game of Go ends when both P1 and P2 agree that there will be no more moves or when either P1 or P2 resigns

    Counting the score
    1. At the end of the game, whichever stones will inevitably be captured are dead
    2. Stones that cannot be captured are alive
    3. All dead stones of both P1 and P2 are removed from the board
    4. All living stones of each player are counted, including the vacant points enclosed by those stones
    5. Vacant points between the living stones of both P1 and P2 will be shared equally

    7. 180½ is half the number of points on the board
    8. Let t denote Pn's total number of living stones and enclosed vacant points
    9. If t > 180½, then Pn wins
    10. If t < 180½, then Pn loses
    11. If t = 180½, then the game has ended in a draw


    1. Go is a far more complex game than chess

      Chess Chinese Chess Shogi Go
    Board size 64 (8 × 8) 90 (9 × 10) 81 (9 × 9) 361 (19 × 19)
    State space complexity 1046 1048 1071 10172
    Game tree complexity 10123 10150 10226 10360
    Branching factor 35 38 92 250


     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .