• Back to Profile
    •  

     

     

     

     

     



    Tic-tac-toe & chess

    Tic-tac-toe (or noughts & crosses)


    The game starts by P1 clicking on one of the cells in the 3 × 3 grid


    P1 (Human) will play as X (crosses)

    P2 (Human) will play as O (noughts)














    Human versus human
    1. Tic-tac-toe is a 2-player sequential zero-sum game with perfect information:
      1. This game is played by exactly 2 players P1 and P2 (2-player);
      2. P1 and P2 take turns to move as opposed to moving simultaneously (sequential);
      3. When a payoff value is assigned to each player in a game-final position (+1 for a win, -1 for a loss, and 0 for a draw), the sum of payoffs for P1 and P2 will be equal to zero (zero-sum)
      4. Both P1 and P2 know the results of all previous moves by P1 and P2 (perfect information



    A partial game tree for Tic-tac-toe

    1. A game tree is the search tree for a game
    2. Each node in the game tree represents a legal position in that game
    3. The root node (with no parents) represents the game-initial position and MAX (P1 or X (crosses)) moves first
    4. As we expand this game tree, MAX (P1) and MIN (P2) take turns to move, until we arrive at the game-final positions
    5. The leaf nodes (with no children) represent the game-final positions
    6. A payoff value is assigned to each player at the game-final position: +1 for a win, −1 for a loss, 0 for a draw)


    1. Tic-tac-toe is a solved game:
    2. Assuming perfect play from both P1 and P2, we can correctly predict the outcome of this game (win, lose, or draw)
    3. More specifically, assuming perfect play from both P1 and P2, the outcome will be a forced draw


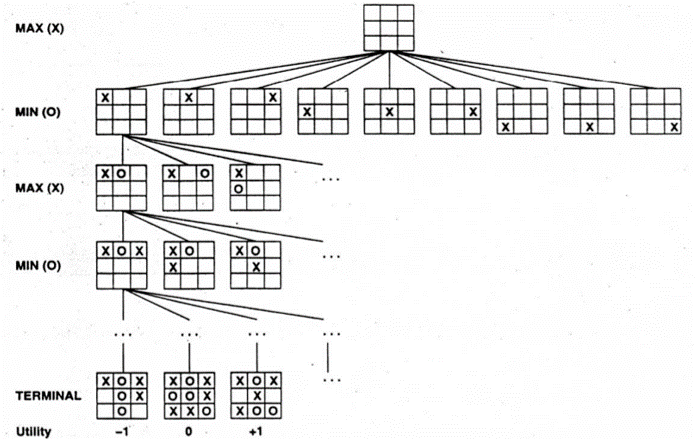
    Chess


    P1 (Human) will play as White
    P1's (or White's) most recent moves are highlighted in dark red

    P2 (AI) will play as Black
    P2's (or Black's) most recent moves are highlighted in cornflower blue

    Suggested moves will be highlighted in teal




    No check, checkmate, or draw.



         

    Human versus AI



    Adapted from Zhang Zeyu's GitHub source code for chess-playing AI




    1. Like tic-tac-toe, chess is a 2-player sequential zero-sum game with perfect information
    2. However, chess is a more complex game than tic-tac-toe
    3. Variants of chess on a smaller board and with fewer pieces have been solved
    4. However, chess itself has not been solved


    1. Combinatorial game theory allows for the complexity of different games to be measured:
    2. State space complexity — the number of legal game positions reachable from the initial state of the game s0;
    3. Game tree complexity — the number of leaf nodes in a game tree rooted at the initial state s0 as the root node;
    4. Branching factor — the average number of legal moves that you can make from a given position si


      Tic-tac-toe Chess
    Board size 9 (3 × 3) 64 (8 × 8)
    State space complexity 103 1046
    Game tree complexity 105 10123
    Branching factor 4 35
     

     

    Background image taken from: https://cdn.asiatatler.com/asiatatler/i/th/2020/02/04101225-aurora-1185464-1920_cover_1920x1280.jpg This website has been coded using html, css, and js and is dedicated to B and H .